<Box-Jenkins 모형>
1. 서론
Box-Jenkins의 ARIMA방법: 시계열을 정상화시키고 자기회귀 모수에 이동평균 모수를 결합하여 예측에 적합한 하나의 통합모형을 구축하는 방법
*평활법/분해법은 고전적인 시계열 기법으로 13,14주차 강의에서 다룰 것임
(평활법: 예측과 추세 계절 조정을 위한 이동평균 및 가중 이동평균에 근거한 외삽법)
(분해법: 시계열을 추세 순환 계절 및 불규칙 성분으로 나누고 예측을 위해 계절 조정된 시계열을 얻기 위해 회귀분석 및 이동평균 기법들을 사용)
확률적 과정에 기초를 둠-> 구조적 변화보다는 점진적 변화를 공식화하는데 적합
ARIMA 모형의 기본전제 조건
[제약조건]
1. 충분한 자료 필요
2. 약한 정상성
3. 등간격으로 수집된 적어도 30-50개의 결측값이 없는 관측 값으로 구성
일부 자료 결측시 결측값을 대체
-전체평균, 결측값 발생 기간 평균값, 주변 관측값들의 중앙값, 인접 관측값의 평균 등으로 대체
ex. use SAS의 PROC EXPAND
/*PROC EXPAND를 이용한 결측값 대체 방법**/
data res_miss;
input yt @@;
date=intnx('year', '01jan1995'd, _n_-1);
format date year4.; /*date의 format은 19??-20?? 형식*/
cards;
37 44 55 53 58 . 48 45 41 34 30 24 /*1995-2006, 결측값은 2000년에*/
;
proc expand data=res_miss out=new from=year method=join;
convert yt=ynew/observed=middle;
id date;
run;
title1 'Interpolated data observed=middle';
title2 'method=join';
proc print data=new;
var date yt ynew;
run;
1) proc expand data=res_miss out=new from=year method=join;
DATA=SAS-data-set: 입력 자료의 이름을 지정
OUT=SAS-data-set: 출력 자료의 이름을 지정
FROM=interval, TO=interval : 입력(출력) 자료에 있는 관측값들 사이의 시간 간격을 지정하는 것으로 YEAR, QTR(분기), MONTH, DAY와 HOUR를 지정할 수 있음
METHOD= option: 시계열을 변환시키는 방법을 지정하는 명령어로 지원되는 방법으로는
SPLINE (default): 3차 다항곡선으로 구성된 연속함수 적합
JOIN: 계속하여 선분을 연결하여 연속적인 곡선 적합
STEP: 불연속 piecewise constant curve 적합
AGGREGATE와 NONE
2) convert yt=ynew / observed=middle;
CONVERT var = newname / option ; 수행될 숫자변수를 지정하는 명령문으로,
선택사항은
OBSERVED=value: 입력 계열과 출력 계열의 관측 값의 특성을 지정하는 명령어로 사용가능한 값은 TOTAL, AVERAGE, BEGINNING(디폴트), MIDDLE, END
3) id date ;
입력 및 출력 자료에 있는 관측 값을 식별하는 숫자 변수를 지정하는 명령문

2. 정상성
시계열 회귀모형의 관점에서 역사적인 관계식이 미래로 일반화되도록 공식화하는데 필요한 개념
시계열의 수준과 분산이 시간에 따라 체계적인 변화가 없고(시계열 변수들의 분포가 시간에 따라 변하지 않는) 미래는 확률적으로 과거와 동일함을 의미
1. E(Yt)=μt=μ
2. Var(Yt)=σ2t=σ2로 일정


:Cov(Yt,Yt+k)가 t에 따라 특정한 양태 없이 시간 간격 k에만 관계함
본 강의에서는주어진 시계열이 가우시안 과정을 따르며 약하게 정상적인 조건을 만족하는 경우에 국한하기로 한다.
* 시계열 {Y_t}가 가우시안 과정이라고 함은 {Y_t}의 분포함수가 모두 다변량 정규분포를 따름을 의미한다.
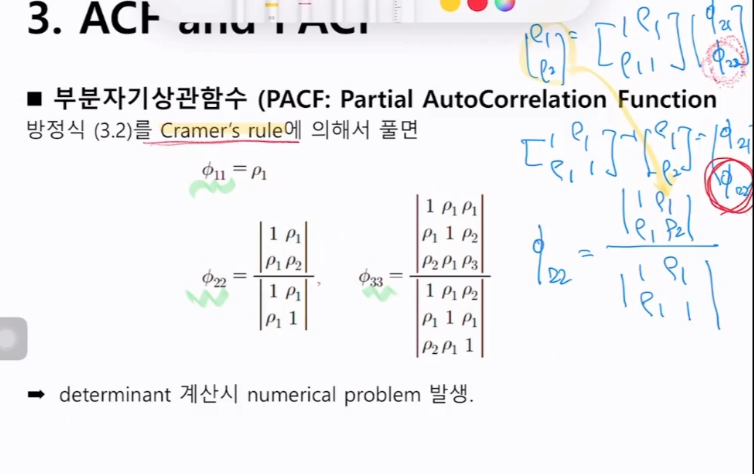
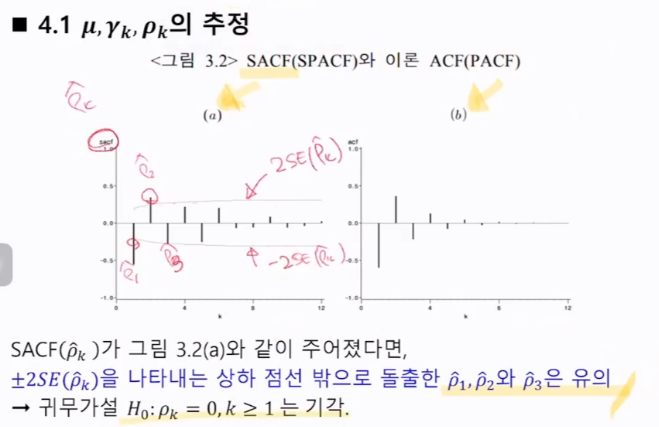
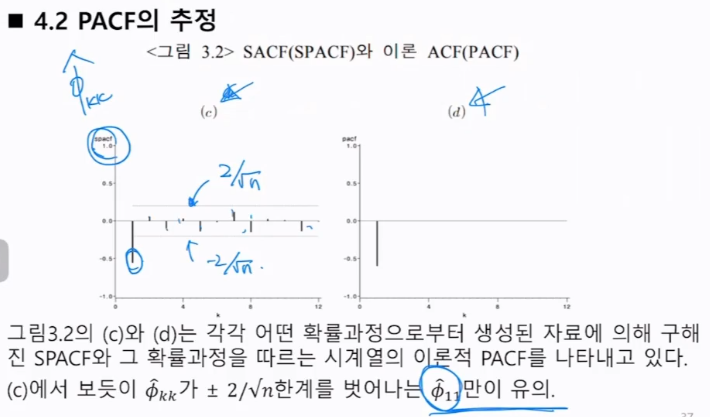
3. 자기상관함수(ACF)와 부분자기상관함수(PACF)

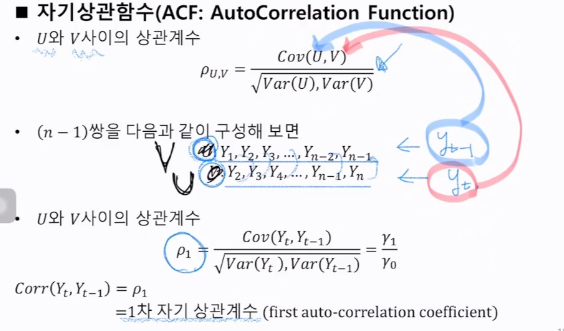

상관도표: 자기상관함수를 주어진 k에 따라서 도표화한 것

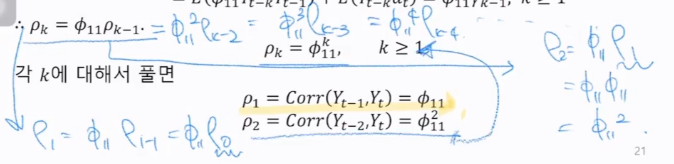






k가 만약에 2라면,

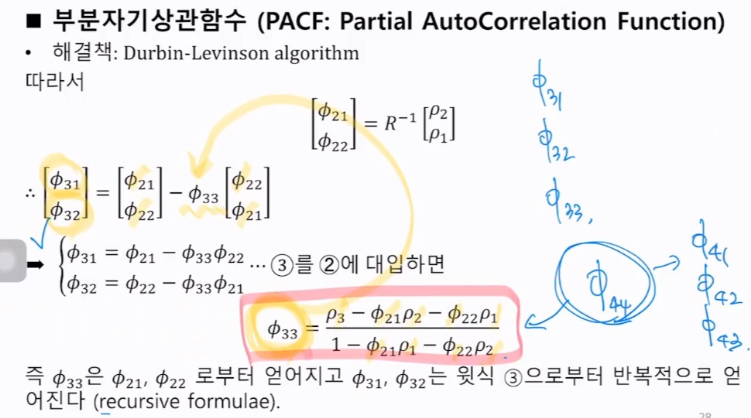
해결책: Durbin-Levinson algorithm



4. ACF와 PACF의 추정





* nlag의 숫자는 일반적으로 n(관측값)의 1/4~1/2정도로 설정
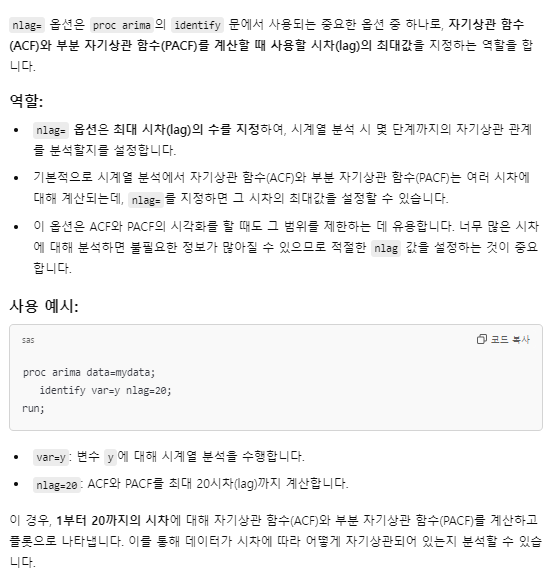

Fig 1_5
data fig1_5;
input yt @@;
t=_n_;
wt=dif(yt);
lines;
2 7 8 9 12 13 15 16 18 19 20
24 25 26 28 31 34 36 39
;
symbol i=join v=cdot;
proc gplot;
plot yt*t wt*t / overlay;
run;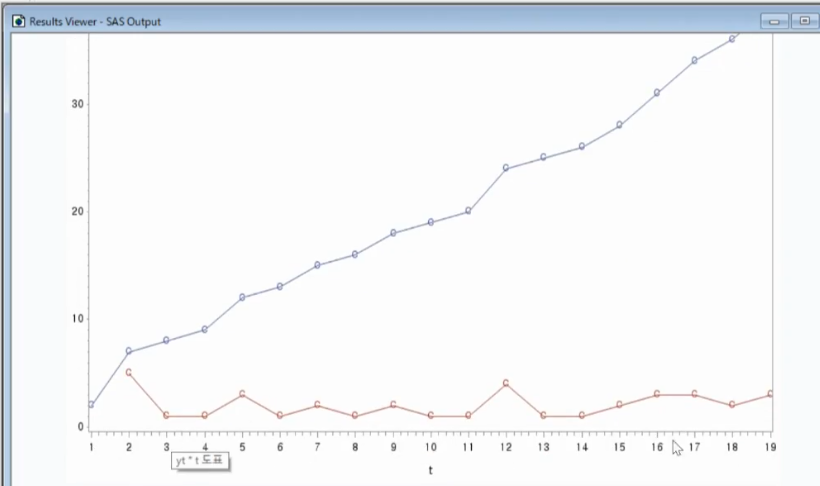
'학교공부 > 시계열자료분석' 카테고리의 다른 글
| 7주차_모형추정 (0) | 2025.01.04 |
|---|---|
| 5,6주차_비정상성 시계열, ARIMA 모형의 성질, 모형식별 (0) | 2025.01.04 |
| 4주차_이동평균모형, 혼합모형의 특성 파악 (0) | 2025.01.04 |
| 3주차 복습_백색잡음과정, 자기회귀모형의 특성 파악 (0) | 2024.10.21 |
| 1주차_OT (0) | 2024.09.02 |